import math
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline- Rederive main backprop pieces after watching Karpathy’s https://www.youtube.com/watch?v=VMj-3S1tku0&ab_channel=AndrejKarpathy
def f(x):
return 3*x**2 - 4*x + 5xs = np.arange(-5,5,0.25)
ys = f(xs)
plt.plot(xs,ys)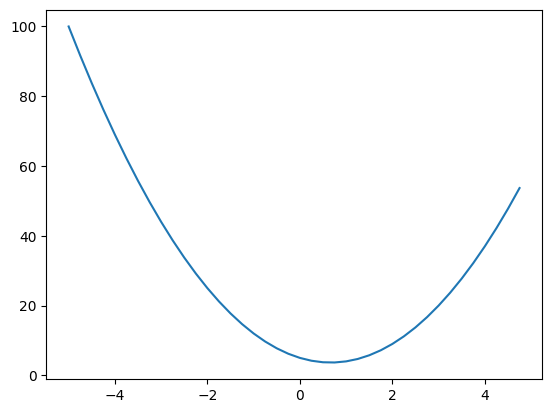
class Value:
def __init__(self,data,_children=(),_op='',label=''):
self.data = data
self.grad = 0.0
self._backward = lambda: None # backward function does not do anything by default
self._prev = set(_children) #set for efficiency, children in the backpropagation sense
self._op = _op
self.label = label
def __repr__(self):
return f"Value(data={self.data})"
def __add__(self,other):
other = other if isinstance(other,Value) else Value(other)
out = Value(self.data+other.data,_children=(self,other),_op='+')
def _backward():
self.grad += 1.0*out.grad
other.grad += 1.0*out.grad
out._backward = _backward
return out
def __mul__(self,other):
other = other if isinstance(other,Value) else Value(other)
out = Value(self.data*other.data,_children=(self,other),_op='*')
def _backward():
# self.grad += other.grad*out.grad #HAD A BUG HERE COULD NOT PROPAGATE GRAD; FIXED BY INVESTIGATING PIECE-BY-PIECE AS SHOULD DO IN FUTURE!
# other.grad += self.grad*out.grad
self.grad += other.data*out.grad
other.grad += self.data*out.grad
out._backward = _backward
return out
def __pow__(self, other):
assert isinstance(other,(int,float))
out = Value(self.data**other,(self,),_op=f'**{other}')
def _backward():
self.grad += (other*self.data**(other-1)) *out.grad
out._backward = _backward
return out
def tanh(self):
x= self.data
t = (math.exp(2*x)-1)/(math.exp(2*x)+1)
out = Value(t,_children=(self,),_op='tanh')
def _backward():
self.grad += (1 - t**2)*out.grad
out._backward = _backward
return out
# exercise: ReLu
def relu(self):
out = Value( self.data if self.data >=0 else 0, _children = (self,), _op='ReLU')
def _backward():
if self.data>=0:
self.grad += out.grad
else:
self.grad = 0
# Karpathy summarized above as self.grad += (out.data > 0) * out.grad
out._backward = _backward
def exp(self):
x= self.data
t = Value(math.exp(2*x), _children=(self,),_op='exp')
def _backward():
self.grad += t*t.grad
t._backward = _backward
return t
def __truediv__(self,other):
return self*other**-1
def backward(self):
topo = []
visited =set()
def build_topo(v):
if v not in visited:
visited.add(v)
for child in v._prev: # FIXED INDENTATION
build_topo(child)
topo.append(v) # add yourself to the list after your children get added to the list
build_topo(self)
self.grad = 1.0
for v in reversed(topo): # Propagating backward
v._backward()
def __neg__(self):
return -1*self
def __sub__(self,other):
return self + (-other)
#Python first check if self, other in __add__ can be added (self must be Value). If cannot, will flip self and other before passing them to __radd__
#Hence __radd__ already gets arguments in flipped order!!!
def __radd__(self,other):
return self+other
def __rsub__(self,other):
return self-other
def __rmul__(self,other):
return self*othera = Value(2.0,label='a')
b = Value(-3.0,label='b')
c = Value(10.0,label='c')
e=a*b; e.label = 'e'
d=e+c; d.label = 'd'
f = Value(-2.0, label='f')
L = d*f; L.label ='Loss'; L.grad=1.0
L.backward()d._prev{Value(data=-6.0), Value(data=10.0)}from graphviz import Digraph
# ME: Note how Andrej used a closure instead of a helper, as I might
def trace(root):
# builds a set of all nodes and edges in a graph
nodes, edges = set(),set()
def build(v):
if v not in edges:
nodes.add(v)
for child in v._prev:
edges.add((child,v))
build(child)
build(root)
return nodes, edges
def draw_dot(root):
dot = Digraph(format='svg', graph_attr={'rankdir':'LR'})
nodes,edges = trace(root)
for n in nodes:
uid = str(id(n))
# for any value in the graph, create a rectangular ('record') node for it
dot.node(name=uid, label="{%s| data %.4f | grad %.4f}" % (n.label,n.data,n.grad), shape='record')
if n._op:
# if this value is a result of some operation, create an op node for it
dot.node(name=uid+n._op, label=n._op)
# and connect this node for it
dot.edge(uid + n._op, uid)
for n1, n2 in edges:
# connect n1 to the op node of n2
dot.edge(str(id(n1)),str(id(n2))+n2._op)
return dotdraw_dot(L)L = d*fL.grad = 1.0def locally_scope():
h=0.001
a = Value(2.0,label='a')
b = Value(-3.0,label='b')
c = Value(10.0,label='c')
e=a*b; e.label = 'e'
d=e+c; d.label = 'd'
f = Value(-2.0, label='f')
L = d*f; L.label ='Loss'
L1 = L.data
a = Value(2.0,label='a')
b = Value(-3.0,label='b')
c = Value(10.0,label='c')
e=a*b; e.label = 'e'
d=e+c; d.label = 'd'
f = Value(-2.0+h, label='f')
L = d*f; L.label ='Loss'
L2 = L.data
print((L2-L1)/h)
locally_scope()3.9999999999995595import random
class Module:
def zero_grad(self):
for p in self.parameters():
p.grad = 0
def parameters(self):
return []
class Neuron(Module):
def __init__(self,nin): #nin: number of inputs/weights to the Neuron
self.w = [Value(random.uniform(-1,1)) for _ in range(nin)]
self.b = Value(random.uniform(-1,1))
def __call__(self,x):
#w*x + b
act = sum((wi*xi for wi,xi in zip(self.w,x)),self.b) #sum takes second argument as start of sum, so start at self.b
out = act.tanh()
return out
def parameters(self):
return self.w +[self.b]
class Layer(Module):
def __init__(self,nin,nout):
self.neurons = [Neuron(nin) for _ in range(nout)]
def __call__(self,x):
outs = [n(x) for n in self.neurons] # call each neuron on data
return outs[0] if len(outs) == 1 else outs
def parameters(self):
return [p for neuron in self.neurons for p in neuron.parameters()]
class MLP(Module):
def __init__(self,nin,nouts): # a list of nouts defining the sizes of all the layers in MLP
sz = [nin] + nouts # [3,4,4,1] in example from picture
self.layers = [Layer(sz[i],sz[i+1]) for i in range(len(nouts))] #sz is len(nouts) + 1!
def __call__(self,x):
for layer in self.layers:
x = layer(x) #going through and applying layer() to previous input
#print(x)
return x
def parameters(self):
return [p for layer in self.layers for p in layer.parameters()] #Notice how loops are ordered in same order as usual!!!
x = [2.0, 3.0]
n = Neuron(2)
print('n(x): ', n(x))
l = Layer(2,3)
print('l(x): ', l(x))
x = [2.0, 3.0, -1.0]
m = MLP(3, [4,4,1])
print('m(x): ', m(x))n(x): Value(data=-0.9830138790054755)
l(x): [Value(data=0.7705154949040606), Value(data=0.7657867069400349), Value(data=0.9990156183039722)]
m(x): Value(data=-0.3627764910030339)draw_dot(m(x))xs =[
[2.0, 3.0, -1.0],
[3.0,-1.0,0.5],
[0.5,1.0,1.0],
[1.0,1.0,-1.0]
]
ys = [1.0, -1.0, -1.0, 1.0]
ypred = [m(x) for x in xs]
ypred[Value(data=-0.3627764910030339),
Value(data=-0.37942407700946207),
Value(data=-0.34471593548870183),
Value(data=-0.2922952263934983)]#loss = sum([(yout-ygt)**2 for ygt,yout in zip(ys,ypred)])
loss = sum([(ygt-yout)**2 for ygt,yout in zip(ys,ypred)])
# ygt: y ground truth; order of subtraction important unless define __rsub__, as I did above
# deleted Layer and reran class initialization for Neuron, etc, to make this change take effectlossValue(data=4.341698397987971)loss.grad=1.0loss.backward()draw_dot(loss)m.layers[0].neurons[0].w[0].grad0.012225375750811174len(m.parameters())
for p in m.parameters():
p.data += -0.01*p.gradm.layers[0].neurons[0].w[0].grad0.012225375750811174ypred[Value(data=-0.3627764910030339),
Value(data=-0.37942407700946207),
Value(data=-0.34471593548870183),
Value(data=-0.2922952263934983)]# Building a training loop
xs =[
[2.0, 3.0, -1.0],
[3.0,-1.0,0.5],
[0.5,1.0,1.0],
[1.0,1.0,-1.0]
]
ys = [1.0, -1.0, -1.0, 1.0]
ITERS = 100
for k in range(ITERS):
#forward pass
ypred = [m(x) for x in xs]
loss = sum((ygt-yout)**2 for ygt,yout in zip(ys,ypred))
if k == 0: loss.grad = 1.0
#backward pass
for p in m.parameters(): # Don't double accumulate; the backward pass is taking care of accumulation with += (counteracting overwriting derivs if same variable in multiple places)
p.grad = 0.0
loss.backward()
# update
for p in m.parameters(): # m.parameters!!! Had n.parameters. FOR FUTURE, KEEP SAME NOTATION AS PRESENTER TO SAVE MY TIME!!!
p.data += -0.05 * p.grad
#print(k,loss.data)
#ypreddraw_dot(loss)